tuning_playbook - A playbook for systematically maximizing the performance of deep learning models.
Deep Learning Tuning Playbook
This is not an officially supported Google product.
Varun Godbole†, George E. Dahl†, Justin Gilmer†, Christopher J. Shallue‡, Zachary Nado†
† Google Research, Brain Team
‡ Harvard University
Table of Contents
- Who is this document for?
- Why a tuning playbook?
- Guide for starting a new project
- A scientific approach to improving model performance
- Determining the number of steps for each training run
- Additional guidance for the training pipeline
- FAQs
- Acknowledgments
- Citing
- Contributing
Who is this document for?
This document is for engineers and researchers (both individuals and teams) interested in maximizing the performance of deep learning models. We assume basic knowledge of machine learning and deep learning concepts.
Our emphasis is on the process of hyperparameter tuning. We touch on other aspects of deep learning training, such as pipeline implementation and optimization, but our treatment of those aspects is not intended to be complete.
We assume the machine learning problem is a supervised learning problem or something that looks a lot like one (e.g. self-supervised). That said, some of the prescriptions in this document may also apply to other types of problems.
Why a tuning playbook?
Currently, there is an astonishing amount of toil and guesswork involved in actually getting deep neural networks to work well in practice. Even worse, the actual recipes people use to get good results with deep learning are rarely documented. Papers gloss over the process that led to their final results in order to present a cleaner story, and machine learning engineers working on commercial problems rarely have time to take a step back and generalize their process. Textbooks tend to eschew practical guidance and prioritize fundamental principles, even if their authors have the necessary experience in applied work to provide useful advice. When preparing to create this document, we couldn't find any comprehensive attempt to actually explain how to get good results with deep learning. Instead, we found snippets of advice in blog posts and on social media, tricks peeking out of the appendix of research papers, occasional case studies about one particular project or pipeline, and a lot of confusion. There is a vast gulf between the results achieved by deep learning experts and less skilled practitioners using superficially similar methods. At the same time, these very experts readily admit some of what they do might not be well-justified. As deep learning matures and has a larger impact on the world, the community needs more resources covering useful recipes, including all the practical details that can be so critical for obtaining good results.
We are a team of five researchers and engineers who have worked in deep learning for many years, some of us since as early as 2006. We have applied deep learning to problems in everything from speech recognition to astronomy, and learned a lot along the way. This document grew out of our own experience training neural networks, teaching new machine learning engineers, and advising our colleagues on the practice of deep learning. Although it has been gratifying to see deep learning go from a machine learning approach practiced by a handful of academic labs to a technology powering products used by billions of people, deep learning is still in its infancy as an engineering discipline and we hope this document encourages others to help systematize the field's experimental protocols.
This document came about as we tried to crystalize our own approach to deep learning and thus it represents the opinions of the authors at the time of writing, not any sort of objective truth. Our own struggles with hyperparameter tuning made it a particular focus of our guidance, but we also cover other important issues we have encountered in our work (or seen go wrong). Our intention is for this work to be a living document that grows and evolves as our beliefs change. For example, the material on debugging and mitigating training failures would not have been possible for us to write two years ago since it is based on recent results and ongoing investigations. Inevitably, some of our advice will need to be updated to account for new results and improved workflows. We do not know the optimal deep learning recipe, but until the community starts writing down and debating different procedures, we cannot hope to find it. To that end, we would encourage readers who find issues with our advice to produce alternative recommendations, along with convincing evidence, so we can update the playbook. We would also love to see alternative guides and playbooks that might have different recommendations so we can work towards best practices as a community. Finally, any sections marked with a 🤖 emoji are places we would like to do more research. Only after trying to write this playbook did it become completely clear how many interesting and neglected research questions can be found in the deep learning practitioner's workflow.
Guide for starting a new project
Many of the decisions we make over the course of tuning can be made once at the beginning of a project and only occasionally revisited when circumstances change.
Our guidance below makes the following assumptions:
- Enough of the essential work of problem formulation, data cleaning, etc. has already been done that spending time on the model architecture and training configuration makes sense.
- There is already a pipeline set up that does training and evaluation, and it is easy to execute training and prediction jobs for various models of interest.
- The appropriate metrics have been selected and implemented. These should be as representative as possible of what would be measured in the deployed environment.
Choosing the model architecture
Summary: When starting a new project, try to reuse a model that already works.
- Choose a well established, commonly used model architecture to get working first. It is always possible to build a custom model later.
- Model architectures typically have various hyperparameters that determine
the model's size and other details (e.g. number of layers, layer width, type
of activation function).
- Thus, choosing the architecture really means choosing a family of different models (one for each setting of the model hyperparameters).
- We will consider the problem of choosing the model hyperparameters in Choosing the initial configuration and A scientific approach to improving model performance.
- When possible, try to find a paper that tackles something as close as possible to the problem at hand and reproduce that model as a starting point.
Choosing the optimizer
Summary: Start with the most popular optimizer for the type of problem at hand.
- No optimizer is the "best" across all types of machine learning problems and model architectures. Even just comparing the performance of optimizers is a difficult task. 🤖
- We recommend sticking with well-established, popular optimizers, especially
when starting a new project.
- Ideally, choose the most popular optimizer used for the same type of problem.
- Be prepared to give attention to *all* hyperparameters of the
chosen optimizer.
- Optimizers with more hyperparameters may require more tuning effort to find the best configuration.
- This is particularly relevant in the beginning stages of a project when we are trying to find the best values of various other hyperparameters (e.g. architecture hyperparameters) while treating optimizer hyperparameters as nuisance parameters.
- It may be preferable to start with a simpler optimizer (e.g. SGD with fixed momentum or Adam with fixed $\epsilon$, $\beta_{1}$, and $\beta_{2}$) in the initial stages of the project and switch to a more general optimizer later.
- Well-established optimizers that we like include (but are not limited to):
- SGD with momentum (we like the Nesterov variant)
- Adam and NAdam, which are more general than SGD with momentum. Note that Adam has 4 tunable hyperparameters and they can all matter!
Choosing the batch size
Summary: The batch size governs the training speed and shouldn't be used to directly tune the validation set performance. Often, the ideal batch size will be the largest batch size supported by the available hardware.
- The batch size is a key factor in determining the training time and computing resource consumption.
- Increasing the batch size will often reduce the training time. This can be
highly beneficial because it, e.g.:
- Allows hyperparameters to be tuned more thoroughly within a fixed time interval, potentially resulting in a better final model.
- Reduces the latency of the development cycle, allowing new ideas to be tested more frequently.
- Increasing the batch size may either decrease, increase, or not change the resource consumption.
- The batch size should not be treated as a tunable hyperparameter for
validation set performance.
- As long as all hyperparameters are well-tuned (especially the learning rate and regularization hyperparameters) and the number of training steps is sufficient, the same final performance should be attainable using any batch size (see Shallue et al. 2018).
- Please see Why shouldn't the batch size be tuned to directly improve validation set performance?
Determining the feasible batch sizes and estimating training throughput
[Click to expand]
- For a given model and optimizer, there will typically be a range of batch sizes supported by the available hardware. The limiting factor is usually accelerator memory.
- Unfortunately, it can be difficult to calculate which batch sizes will fit in memory without running, or at least compiling, the full training program.
- The easiest solution is usually to run training jobs at different batch sizes (e.g. increasing powers of 2) for a small number of steps until one of the jobs exceeds the available memory.
- For each batch size, we should train for long enough to get a reliable estimate of the training throughput
training throughput = (# examples processed per second)
or, equivalently, the time per step.
time per step = (batch size) / (training throughput)
- When the accelerators aren't yet saturated, if the batch size doubles, the training throughput should also double (or at least nearly double). Equivalently, the time per step should be constant (or at least nearly constant) as the batch size increases.
- If this is not the case then the training pipeline has a bottleneck such as I/O or synchronization between compute nodes. This may be worth diagnosing and correcting before proceeding.
- If the training throughput increases only up to some maximum batch size,
then we should only consider batch sizes up to that maximum batch size, even
if a larger batch size is supported by the hardware.
- All benefits of using a larger batch size assume the training throughput increases. If it doesn't, fix the bottleneck or use the smaller batch size.
- Gradient accumulation simulates a larger batch size than the hardware can support and therefore does not provide any throughput benefits. It should generally be avoided in applied work.
- These steps may need to be repeated every time the model or optimizer is changed (e.g. a different model architecture may allow a larger batch size to fit in memory).
Choosing the batch size to minimize training time
[Click to expand]
Training time = (time per step) x (total number of steps)
- We can often consider the time per step to be approximately constant for all feasible batch sizes. This is true when there is no overhead from parallel computations and all training bottlenecks have been diagnosed and corrected (see the previous section for how to identify training bottlenecks). In practice, there is usually at least some overhead from increasing the batch size.
- As the batch size increases, the total number of steps needed to reach a
fixed performance goal typically decreases (provided all relevant
hyperparameters are re-tuned when the batch size is changed;
Shallue et al. 2018).
- E.g. Doubling the batch size might halve the total number of steps required. This is called perfect scaling.
- Perfect scaling holds for all batch sizes up to a critical batch size, beyond which one achieves diminishing returns.
- Eventually, increasing the batch size no longer reduces the number of training steps (but never increases it).
- Therefore, the batch size that minimizes training time is usually the
largest batch size that still provides a reduction in the number of training
steps required.
- This batch size depends on the dataset, model, and optimizer, and it is an open problem how to calculate it other than finding it experimentally for every new problem. 🤖
- When comparing batch sizes, beware the distinction between an example
budget/epoch
budget (running all experiments while fixing the number of training
example presentations) and a step budget (running all experiments with
the number of training steps fixed).
- Comparing batch sizes with an epoch budget only probes the perfect scaling regime, even when larger batch sizes might still provide a meaningful speedup by reducing the number of training steps required.
- Often, the largest batch size supported by the available hardware will be smaller than the critical batch size. Therefore, a good rule of thumb (without running any experiments) is to use the largest batch size possible.
- There is no point in using a larger batch size if it ends up increasing the training time.
Choosing the batch size to minimize resource consumption
[Click to expand]
- There are two types of resource costs associated with increasing the batch
size:
- Upfront costs, e.g. purchasing new hardware or rewriting the training pipeline to implement multi-GPU / multi-TPU training.
- Usage costs, e.g. billing against the team's resource budgets, billing from a cloud provider, electricity / maintenance costs.
- If there are significant upfront costs to increasing the batch size, it might be better to defer increasing the batch size until the project has matured and it is easier to assess the cost-benefit tradeoff. Implementing multi-host parallel training programs can introduce bugs and subtle issues so it is probably better to start off with a simpler pipeline anyway. (On the other hand, a large speedup in training time might be very beneficial early in the process when a lot of tuning experiments are needed).
- We refer to the total usage cost (which may include multiple different kinds of costs) as the "resource consumption". We can break down the resource consumption into the following components:
Resource consumption = (resource consumption per step) x (total number of steps)
- Increasing the batch size usually allows us to
reduce the total number of steps.
Whether the resource consumption increases or decreases will depend on how
the consumption per step changes.
- Increasing the batch size might decrease the resource consumption. For example, if each step with the larger batch size can be run on the same hardware as the smaller batch size (with only a small increase in time per step), then any increase in the resource consumption per step might be outweighed by the decrease in the number of steps.
- Increasing the batch size might not change the resource consumption. For example, if doubling the batch size halves the number of steps required and doubles the number of GPUs used, the total consumption (in terms of GPU-hours) will not change.
- Increasing the batch size might increase the resource consumption. For example, if increasing the batch size requires upgraded hardware, the increase in consumption per step might outweigh the reduction in the number of steps.
Changing the batch size requires re-tuning most hyperparameters
[Click to expand]
- The optimal values of most hyperparameters are sensitive to the batch size. Therefore, changing the batch size typically requires starting the tuning process all over again.
- The hyperparameters that interact most strongly with the batch size, and therefore are most important to tune separately for each batch size, are the optimizer hyperparameters (e.g. learning rate, momentum) and the regularization hyperparameters.
- Keep this in mind when choosing the batch size at the start of a project. If you need to switch to a different batch size later on, it might be difficult, time consuming, and expensive to re-tune everything for the new batch size.
How batch norm interacts with the batch size
[Click to expand]
- Batch norm is complicated and, in general, should use a different batch size than the gradient computation to compute statistics. See the batch norm section for a detailed discussion.
Choosing the initial configuration
- Before beginning hyperparameter tuning we must determine the starting point. This includes specifying (1) the model configuration (e.g. number of layers), (2) the optimizer hyperparameters (e.g. learning rate), and (3) the number of training steps.
- Determining this initial configuration will require some manually configured training runs and trial-and-error.
- Our guiding principle is to find a simple, relatively fast, relatively
low-resource-consumption configuration that obtains a "reasonable" result.
- "Simple" means avoiding bells and whistles wherever possible; these can
always be added later. Even if bells and whistles prove helpful down the
road, adding them in the initial configuration risks wasting time tuning
unhelpful features and/or baking in unnecessary complications.
- For example, start with a constant learning rate before adding fancy decay schedules.
- Choosing an initial configuration that is fast and consumes minimal
resources will make hyperparameter tuning much more efficient.
- For example, start with a smaller model.
- "Reasonable" performance depends on the problem, but at minimum means that the trained model performs much better than random chance on the validation set (although it might be bad enough to not be worth deploying).
- "Simple" means avoiding bells and whistles wherever possible; these can
always be added later. Even if bells and whistles prove helpful down the
road, adding them in the initial configuration risks wasting time tuning
unhelpful features and/or baking in unnecessary complications.
- Choosing the number of training steps involves balancing the following
tension:
- On the one hand, training for more steps can improve performance and makes hyperparameter tuning easier (see Shallue et al. 2018).
- On the other hand, training for fewer steps means that each training run is faster and uses fewer resources, boosting tuning efficiency by reducing the time between cycles and allowing more experiments to be run in parallel. Moreover, if an unnecessarily large step budget is chosen initially, it might be hard to change it down the road, e.g. once the learning rate schedule is tuned for that number of steps.
A scientific approach to improving model performance
For the purposes of this document, the ultimate goal of machine learning development is to maximize the utility of the deployed model. Even though many aspects of the development process differ between applications (e.g. length of time, available computing resources, type of model), we can typically use the same basic steps and principles on any problem.
Our guidance below makes the following assumptions:
- There is already a fully-running training pipeline along with a configuration that obtains a reasonable result.
- There are enough computational resources available to conduct meaningful tuning experiments and run at least several training jobs in parallel.
The incremental tuning strategy
Summary: Start with a simple configuration and incrementally make improvements while building up insight into the problem. Make sure that any improvement is based on strong evidence to avoid adding unnecessary complexity.
- Our ultimate goal is to find a configuration that maximizes the performance
of our model.
- In some cases, our goal will be to maximize how much we can improve the model by a fixed deadline (e.g. submitting to a competition).
- In other cases, we want to keep improving the model indefinitely (e.g. continually improving a model used in production).
- In principle, we could maximize performance by using an algorithm to
automatically search the entire space of possible configurations, but this
is not a practical option.
- The space of possible configurations is extremely large and there are not yet any algorithms sophisticated enough to efficiently search this space without human guidance.
- Most automated search algorithms rely on a hand-designed search space that defines the set of configurations to search in, and these search spaces can matter quite a bit.
- The most effective way to maximize performance is to start with a simple
configuration and incrementally add features and make improvements while
building up insight into the problem.
- We use automated search algorithms in each round of tuning and continually update our search spaces as our understanding grows.
- As we explore, we will naturally find better and better configurations and
therefore our "best" model will continually improve.
- We call it a launch when we update our best configuration (which may or may not correspond to an actual launch of a production model).
- For each launch, we must make sure that the change is based on strong evidence – not just random chance based on a lucky configuration – so that we don't add unnecessary complexity to the training pipeline.
At a high level, our incremental tuning strategy involves repeating the following four steps:
- Identify an appropriately-scoped goal for the next round of experiments.
- Design and run a set of experiments that makes progress towards this goal.
- Learn what we can from the results.
- Consider whether to launch the new best configuration.
The remainder of this section will consider this strategy in much greater detail.
Exploration vs exploitation
Summary: Most of the time, our primary goal is to gain insight into the problem.
- Although one might think we would spend most of our time trying to maximize
performance on the validation set, in practice we spend the majority of our
time trying to gain insight into the problem, and comparatively little time
greedily focused on the validation error.
- In other words, we spend most of our time on "exploration" and only a small amount on "exploitation".
- In the long run, understanding the problem is critical if we want to
maximize our final performance. Prioritizing insight over short term gains
can help us:
- Avoid launching unnecessary changes that happened to be present in well-performing runs merely through historical accident.
- Identify which hyperparameters the validation error is most sensitive to, which hyperparameters interact the most and therefore need to be re-tuned together, and which hyperparameters are relatively insensitive to other changes and can therefore be fixed in future experiments.
- Suggest potential new features to try, such as new regularizers if overfitting is an issue.
- Identify features that don't help and therefore can be removed, reducing the complexity of future experiments.
- Recognize when improvements from hyperparameter tuning have likely saturated.
- Narrow our search spaces around the optimal value to improve tuning efficiency.
- When we are eventually ready to be greedy, we can focus purely on the validation error even if the experiments aren't maximally informative about the structure of the tuning problem.
Choosing the goal for the next round of experiments
Summary: Each round of experiments should have a clear goal and be sufficiently narrow in scope that the experiments can actually make progress towards the goal.
- Each round of experiments should have a clear goal and be sufficiently narrow in scope that the experiments can actually make progress towards the goal: if we try to add multiple features or answer multiple questions at once, we may not be able to disentangle the separate effects on the results.
- Example goals include:
- Try a potential improvement to the pipeline (e.g. a new regularizer, preprocessing choice, etc.).
- Understand the impact of a particular model hyperparameter (e.g. the activation function)
- Greedily minimize validation error.
Designing the next round of experiments
Summary: Identify which hyperparameters are scientific, nuisance, and fixed hyperparameters for the experimental goal. Create a sequence of studies to compare different values of the scientific hyperparameters while optimizing over the nuisance hyperparameters. Choose the search space of nuisance hyperparameters to balance resource costs with scientific value.
Identifying scientific, nuisance, and fixed hyperparameters
[Click to expand]
- For a given goal, all hyperparameters will be either scientific
hyperparameters, nuisance hyperparameters, or fixed
hyperparameters.
- Scientific hyperparameters are those whose effect on the model's performance we're trying to measure.
- Nuisance hyperparameters are those that need to be optimized over in order to fairly compare different values of the scientific hyperparameters. This is similar to the statistical concept of nuisance parameters.
- Fixed hyperparameters will have their values fixed in the current round
of experiments. These are hyperparameters whose values do not need to
(or we do not want them to) change when comparing different values of
the scientific hyperparameters.
- By fixing certain hyperparameters for a set of experiments, we must accept that conclusions derived from the experiments might not be valid for other settings of the fixed hyperparameters. In other words, fixed hyperparameters create caveats for any conclusions we draw from the experiments.
- For example, if our goal is to "determine whether a model with more hidden
layers will reduce validation error", then the number of hidden layers is a
scientific hyperparameter.
- The learning rate is a nuisance hyperparameter because we can only fairly compare models with different numbers of hidden layers if the learning rate is tuned separately for each number of layers (the optimal learning rate generally depends on the model architecture).
- The activation function could be a fixed hyperparameter if we have determined in prior experiments that the best choice of activation function is not sensitive to model depth, or if we are willing to limit our conclusions about the number of hidden layers to only cover this specific choice of activation function. Alternatively, it could be a nuisance parameter if we are prepared to tune it separately for each number of hidden layers.
- Whether a particular hyperparameter is a scientific hyperparameter, nuisance
hyperparameter, or fixed hyperparameter is not inherent to that
hyperparameter, but changes depending on the experimental goal.
- For example, the choice of activation function could be a scientific hyperparameter (is ReLU or tanh a better choice for our problem?), a nuisance hyperparameter (is the best 5-layer model better than the best 6-layer model when we allow several different possible activation functions?), or a fixed hyperparameter (for ReLU nets, does adding batch normalization in a particular position help?).
- When designing a new round of experiments, we first identify the scientific
hyperparameters for our experimental goal.
- At this stage, we consider all other hyperparameters to be nuisance hyperparameters.
- Next, we convert some of the nuisance hyperparameters into fixed
hyperparameters.
- With limitless resources, we would leave all non-scientific hyperparameters as nuisance hyperparameters so that the conclusions we draw from our experiments are free from caveats about fixed hyperparameter values.
- However, the more nuisance hyperparameters we attempt to tune, the
greater the risk we fail to tune them sufficiently well for each setting
of the scientific hyperparameters and end up reaching the wrong
conclusions from our experiments.
- As described below, we could counter this risk by increasing the computational budget, but often our maximum resource budget is less than would be needed to tune over all non-scientific hyperparameters.
- We choose to convert a nuisance hyperparameter into a fixed
hyperparameter when, in our judgment, the caveats introduced by fixing
it are less burdensome than the cost of including it as a nuisance
hyperparameter.
- The more a given nuisance hyperparameter interacts with the scientific hyperparameters, the more damaging it is to fix its value. For example, the best value of the weight decay strength typically depends on the model size, so comparing different model sizes assuming a single specific value of the weight decay would not be very insightful.
- Although the type we assign to each hyperparameter depends on the
experimental goal, we have the following rules of thumb for certain
categories of hyperparameters:
- Of the various optimizer hyperparameters (e.g. the learning rate,
momentum, learning rate schedule parameters, Adam betas etc.), at least
some of them will be nuisance hyperparameters because they tend to
interact the most with other changes.
- They are rarely scientific hyperparameters because a goal like "what is the best learning rate for the current pipeline?" doesn't give much insight – the best setting could easily change with the next pipeline change anyway.
- Although we might fix some of them occasionally due to resource
constraints or when we have particularly strong evidence that they
don't interact with the scientific parameters, we should generally
assume that optimizer hyperparameters must be tuned separately to
make fair comparisons between different settings of the scientific
hyperparameters, and thus shouldn't be fixed.
- Furthermore, we have no a priori reason to prefer one optimizer hyperparameter value over another (e.g. they don't usually affect the computational cost of forward passes or gradients in any way).
- In contrast, the choice of optimizer is typically a scientific
hyperparameter or fixed hyperparameter.
- It is a scientific hyperparameter if our experimental goal involves making fair comparisons between two or more different optimizers (e.g. "determine which optimizer produces the lowest validation error in a given number of steps").
- Alternatively, we might make it a fixed hyperparameter for a variety of reasons, including (1) prior experiments make us believe that the best optimizer for our problem is not sensitive to current scientific hyperparameters; and/or (2) we prefer to compare values of the scientific hyperparameters using this optimizer because its training curves are easier to reason about; and/or (3) we prefer to use this optimizer because it uses less memory than the alternatives.
- Hyperparameters introduced by a regularization technique are typically
nuisance hyperparameters, but whether or not we include the
regularization technique at all is a scientific or fixed hyperparameter.
- For example, dropout adds code complexity, so when deciding whether
to include it we would make "no dropout" vs "dropout" a scientific
hyperparameter and the dropout rate a nuisance hyperparameter.
- If we decide to add dropout to our pipeline based on this experiment, then the dropout rate would be a nuisance hyperparameter in future experiments.
- For example, dropout adds code complexity, so when deciding whether
to include it we would make "no dropout" vs "dropout" a scientific
hyperparameter and the dropout rate a nuisance hyperparameter.
- Architectural hyperparameters are often scientific or fixed
hyperparameters because architecture changes can affect serving and
training costs, latency, and memory requirements.
- For example, the number of layers is typically a scientific or fixed hyperparameter since it tends to have dramatic consequences for training speed and memory usage.
- Of the various optimizer hyperparameters (e.g. the learning rate,
momentum, learning rate schedule parameters, Adam betas etc.), at least
some of them will be nuisance hyperparameters because they tend to
interact the most with other changes.
- In some cases, the sets of nuisance and fixed hyperparameters will depend on
the values of the scientific hyperparameters.
- For example, suppose we are trying to determine which optimizer out of
Nesterov momentum and Adam results in the lowest validation error. The
scientific hyperparameter is the
optimizer, which takes values{"Nesterov_momentum", "Adam"}. The valueoptimizer="Nesterov_momentum"introduces the nuisance/fixed hyperparameters{learning_rate, momentum}, but the valueoptimizer="Adam"introduces the nuisance/fixed hyperparameters{learning_rate, beta1, beta2, epsilon}. - Hyperparameters that are only present for certain values of the scientific hyperparameters are called conditional hyperparameters.
- We should not assume two conditional hyperparameters are the same just
because they have the same name! In the above example, the conditional
hyperparameter called
learning_rateis a different hyperparameter foroptimizer="Nesterov_momentum"versusoptimizer="Adam". Its role is similar (although not identical) in the two algorithms, but the range of values that work well in each of the optimizers is typically different by several orders of magnitude.
- For example, suppose we are trying to determine which optimizer out of
Nesterov momentum and Adam results in the lowest validation error. The
scientific hyperparameter is the
Creating a set of studies
[Click to expand]
- Once we have identified the scientific and nuisance hyperparameters, we
design a "study" or sequence of studies to make progress towards the
experimental goal.
- A study specifies a set of hyperparameter configurations to be run for subsequent analysis. Each configuration is called a "trial".
- Creating a study typically involves choosing the hyperparameters that will vary across trials, choosing what values those hyperparameters can take on (the "search space"), choosing the number of trials, and choosing an automated search algorithm to sample that many trials from the search space. Alternatively, we could create a study by specifying the set of hyperparameter configurations manually.
- The purpose of the studies is to run the pipeline with different values of the scientific hyperparameters, while at the same time "optimizing away" (or "optimizing over") the nuisance hyperparameters so that comparisons between different values of the scientific hyperparameters are as fair as possible.
- In the simplest case, we would make a separate study for each configuration
of the scientific parameters, where each study tunes over the nuisance
hyperparameters.
- For example, if our goal is to select the best optimizer out of Nesterov
momentum and Adam, we could create one study in which
optimizer="Nesterov_momentum"and the nuisance hyperparameters are{learning_rate, momentum}, and another study in whichoptimizer="Adam"and the nuisance hyperparameters are{learning_rate, beta1, beta2, epsilon}. We would compare the two optimizers by selecting the best performing trial from each study. - We can use any gradient-free optimization algorithm, including methods such as Bayesian optimization or evolutionary algorithms, to optimize over the nuisance hyperparameters, although we prefer to use quasi-random search in the exploration phase of tuning because of a variety of advantages it has in this setting. After exploration concludes, if state-of-the-art Bayesian optimization software is available, that is our preferred choice.
- For example, if our goal is to select the best optimizer out of Nesterov
momentum and Adam, we could create one study in which
- In the more complicated case where we want to compare a large number of
values of the scientific hyperparameters and it is impractical to make that
many independent studies, we can include the scientific parameters in the
same search space as the nuisance hyperparameters and use a search algorithm
to sample values of both the scientific and nuisance hyperparameters in a
single study.
- When taking this approach, conditional hyperparameters can cause problems since it is hard to specify a search space unless the set of nuisance hyperparameters is the same for all values of the scientific hyperparameters.
- In this case, our preference for using quasi-random search over fancier black-box optimization tools is even stronger, since it ensures that we obtain a relatively uniform sampling of values of the scientific hyperparameters. Regardless of the search algorithm, we need to make sure somehow that it searches the scientific parameters uniformly.
Striking a balance between informative and affordable experiments
[Click to expand]
- When designing a study or sequence of studies, we need to allocate a limited
budget in order to adequately achieve the following three desiderata:
- Comparing enough different values of the scientific hyperparameters.
- Tuning the nuisance hyperparameters over a large enough search space.
- Sampling the search space of nuisance hyperparameters densely enough.
- The better we can achieve these three desiderata, the more insight we can
extract from our experiment.
- Comparing as many values of the scientific hyperparameters as possible broadens the scope of the insights we gain from the experiment.
- Including as many nuisance hyperparameters as possible and allowing each
nuisance hyperparameter to vary over as wide a range as possible
increases our confidence that a "good" value of the nuisance
hyperparameters exists in the search space for each configuration of
the scientific hyperparameters.
- Otherwise, we might make unfair comparisons between values of the scientific hyperparameters by not searching possible regions of the nuisance parameter space where better values might lie for some values of the scientific parameters.
- Sampling the search space of nuisance hyperparameters as densely as
possible increases our confidence that any good settings for the
nuisance hyperparameters that happen to exist in our search space will
be found by the search procedure.
- Otherwise, we might make unfair comparisons between values of the scientific parameters due to some values getting luckier with the sampling of the nuisance hyperparameters.
- Unfortunately, improvements in any of these three dimensions require
either increasing the number of trials, and therefore increasing the
resource cost, or finding a way to save resources in one of the other
dimensions.
- Every problem has its own idiosyncrasies and computational constraints, so how to allocate resources across these three desiderata requires some level of domain knowledge.
- After running a study, we always try to get a sense of whether the study tuned the nuisance hyperparameters well enough (i.e. searched a large enough space extensively enough) to fairly compare the scientific hyperparameters (as described in greater detail below).
Extracting insight from experimental results
Summary: In addition to trying to achieve the original scientific goal of each group of experiments, go through a checklist of additional questions and, if issues are discovered, revise the experiments and rerun them.
- Ultimately, each group of experiments has a specific goal and we want to
evaluate the evidence the experiments provide toward that goal.
- However, if we ask the right questions, we will often find issues that
need to be corrected before a given set of experiments can make much
progress towards their original goal.
- If we don’t ask these questions, we may draw incorrect conclusions.
- Since running experiments can be expensive, we also want to take the opportunity to extract other useful insights from each group of experiments, even if these insights are not immediately relevant to the current goal.
- However, if we ask the right questions, we will often find issues that
need to be corrected before a given set of experiments can make much
progress towards their original goal.
- Before analyzing a given set of experiments to make progress toward their
original goal, we should ask ourselves the following additional questions:
-
Is the search space large enough?
- If the optimal point from a study is near the boundary of the search space in one or more dimensions, the search is probably not wide enough. In this case, we should run another study with an expanded search space.
-
Have we sampled enough points from the search space?
- If not, run more points or be less ambitious in the tuning goals.
- What fraction of the trials in each study are infeasible (i.e.
trials that diverge, get really bad loss values, or fail to run at all
because they violate some implicit constraint)?
- When a very large fraction of points in a study are infeasible we should try to adjust the search space to avoid sampling such points, which sometimes requires reparameterizing the search space.
- In some cases, a large number of infeasible points can indicate a bug in the training code.
- Does the model exhibit optimization issues?
-
What can we learn from the training curves of the best trials?
- For example, do the best trials have training curves consistent with problematic overfitting?
-
Is the search space large enough?
- If necessary, based on the answers to the questions above, refine the most recent study (or group of studies) to improve the search space and/or sample more trials, or take some other corrective action.
- Once we have answered the above questions, we can move on to evaluating the evidence the experiments provide towards our original goal (for example, evaluating whether a change is useful).
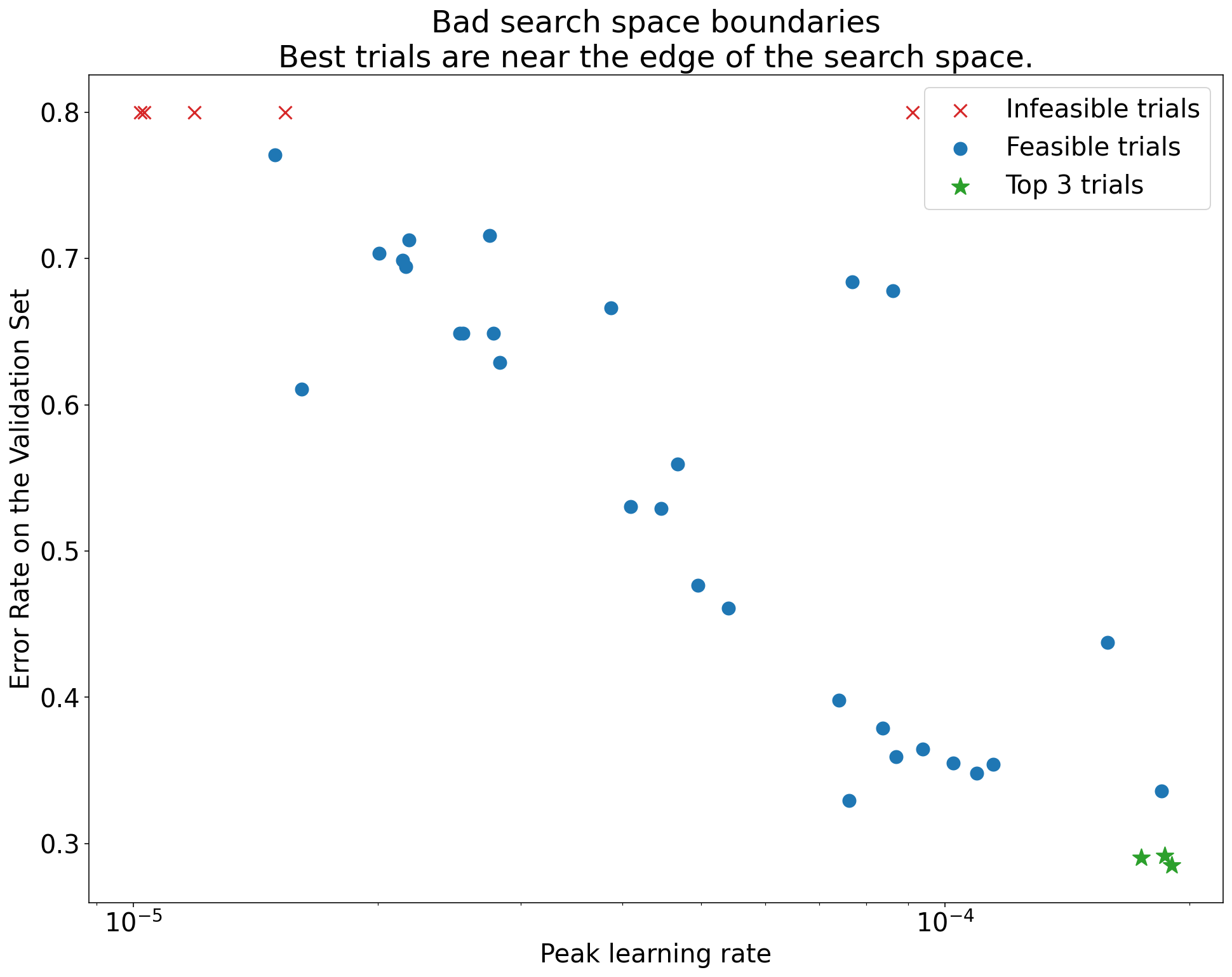
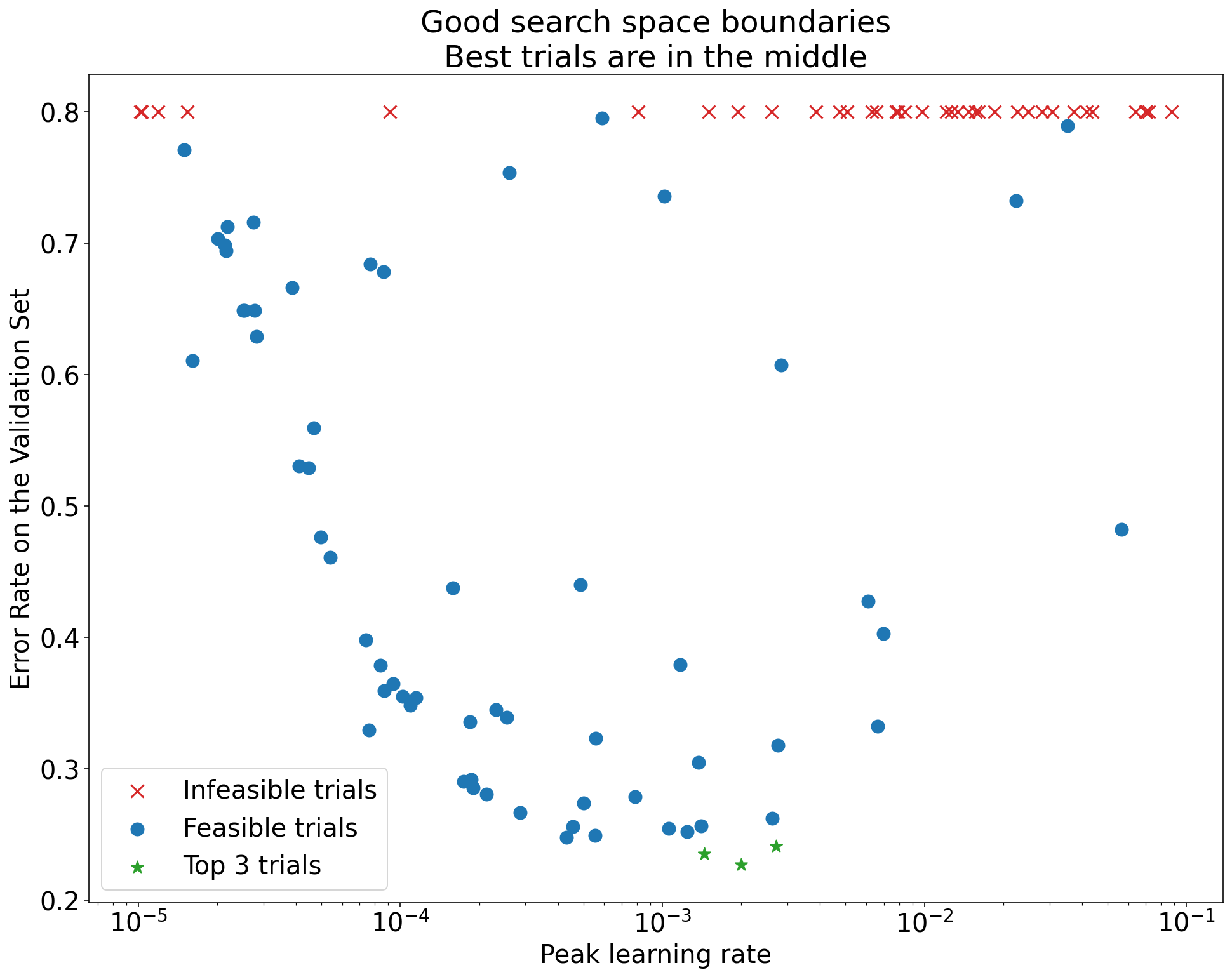
Identifying bad search space boundaries
[Click to expand]
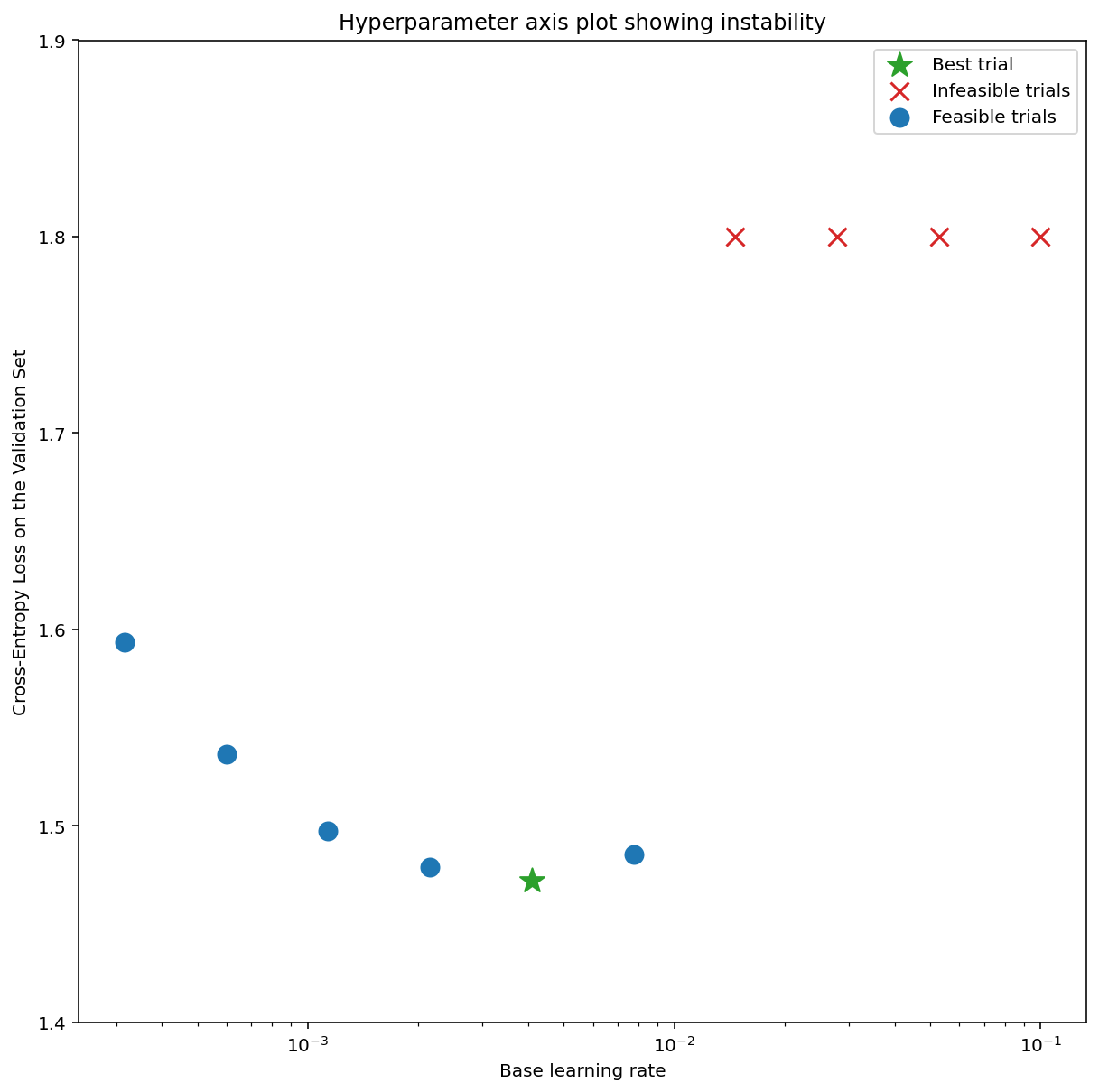
- A search space is suspicious if the best point sampled from it is close to its boundary. We might find an even better point if we expanded the search range in that direction.
- To check search space boundaries, we like to plot completed trials on what
we call basic hyperparameter axis plots where we plot the validation
objective value versus one of the hyperparameters (e.g. learning rate). Each
point on the plot corresponds to a single trial.
- The validation objective value for each trial should usually be the best value it achieved over the course of training.
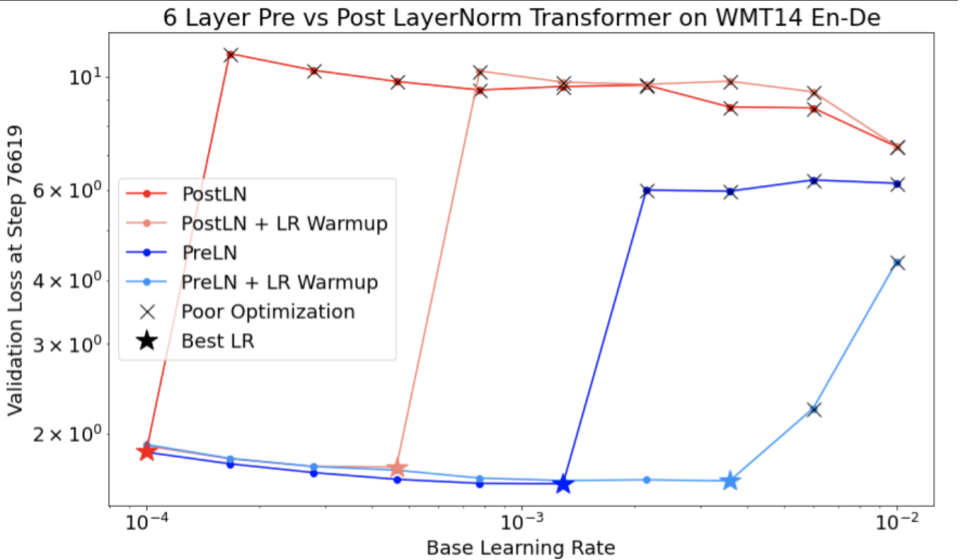
Figure 1: Examples of bad search space boundaries and acceptable search space boundaries.
- The plots in Figure 1 show the error rate (lower is better) against the initial learning rate.
- If the best points cluster towards the edge of a search space (in some dimension), then the search space boundaries might need to be expanded until the best observed point is no longer close to the boundary.
- Often, a study will include "infeasible" trials that diverge or get very bad
results (marked with red Xs in the above plots).
- If all trials are infeasible for learning rates greater than some threshold value, and if the best performing trials have learning rates at the edge of that region, the model may suffer from stability issues preventing it from accessing higher learning rates.
Not sampling enough points in the search space
[Click to expand]
- In general, it can be very difficult to know if the search space has been sampled densely enough. 🤖
- Running more trials is of course better, but comes at an obvious cost.
- Since it is so hard to know when we have sampled enough, we usually sample what we can afford and try to calibrate our intuitive confidence from repeatedly looking at various hyperparameter axis plots and trying to get a sense of how many points are in the "good" region of the search space.
Examining the training curves
[Click to expand]
Summary: Examining the training curves is an easy way to identify common failure modes and can help us prioritize what actions to take next.
- Although in many cases the primary objective of our experiments only requires considering the validation error of each trial, we must be careful when reducing each trial to a single number because it can hide important details about what’s going on below the surface.
- For every study, we always look at the training curves (training error and validation error plotted versus training step over the duration of training) of at least the best few trials.
- Even if this is not necessary for addressing the primary experimental objective, examining the training curves is an easy way to identify common failure modes and can help us prioritize what actions to take next.
- When examining the training curves, we are interested in the following questions.
- Are any of the trials exhibiting problematic overfitting?
- Problematic overfitting occurs when the validation error starts increasing at some point during training.
- In experimental settings where we optimize away nuisance hyperparameters
by selecting the "best" trial for each setting of the scientific
hyperparameters, we should check for problematic overfitting in at
least each of the best trials corresponding to the settings of the
scientific hyperparameters that we’re comparing.
- If any of the best trials exhibits problematic overfitting, we
usually want to re-run the experiment with additional regularization
techniques and/or better tune the existing regularization parameters
before comparing the values of the scientific hyperparameters.
- This may not apply if the scientific hyperparameters include regularization parameters, since then it would not be surprising if low-strength settings of those regularization parameters resulted in problematic overfitting.
- Reducing overfitting is often straightforward using common regularization techniques that add minimal code complexity or extra computation (e.g. dropout, label smoothing, weight decay), so it’s usually no big deal to add one or more of these to the next round of experiments.
- For example, if the scientific hyperparameter is "number of hidden layers" and the best trial that uses the largest number of hidden layers exhibited problematic overfitting, then we would usually prefer to try it again with additional regularization instead of immediately selecting the smaller number of hidden layers.
- Even if none of the "best" trials are exhibiting problematic
overfitting, there might still be a problem if it occurs in any of
the trials.
- Selecting the best trial suppresses configurations exhibiting problematic overfitting and favors those that do not. In other words, it will favor configurations with more regularization.
- However, anything that makes training worse can act as a regularizer, even if it wasn't intended that way. For example, choosing a smaller learning rate can regularize training by hobbling the optimization process, but we typically don't want to choose the learning rate this way.
- So we must be aware that the "best" trial for each setting of the scientific hyperparameters might be selected in such a way that favors "bad" values of some of the scientific or nuisance hyperparameters.
- If any of the best trials exhibits problematic overfitting, we
usually want to re-run the experiment with additional regularization
techniques and/or better tune the existing regularization parameters
before comparing the values of the scientific hyperparameters.
- Is there high step-to-step variance in the training or validation error late
in training?
- If so, this could interfere with our ability to compare different values of the scientific hyperparameters (since each trial randomly ends on a "lucky" or "unlucky" step) and our ability to reproduce the result of the best trial in production (since the production model might not end on the same "lucky" step as in the study).
- The most likely causes of step-to-step variance are batch variance (from randomly sampling examples from the training set for each batch), small validation sets, and using a learning rate that’s too high late in training.
- Possible remedies include increasing the batch size, obtaining more validation data, using learning rate decay, or using Polyak averaging.
- Are the trials still improving at the end of training?
- If so, this indicates that we are in the "compute bound" regime and we may benefit from increasing the number of training steps or changing the learning rate schedule.
- Has performance on the training and validation sets saturated long before
the final training step?
- If so, this indicates that we are in the "not compute-bound" regime and that we may be able to decrease the number of training steps.
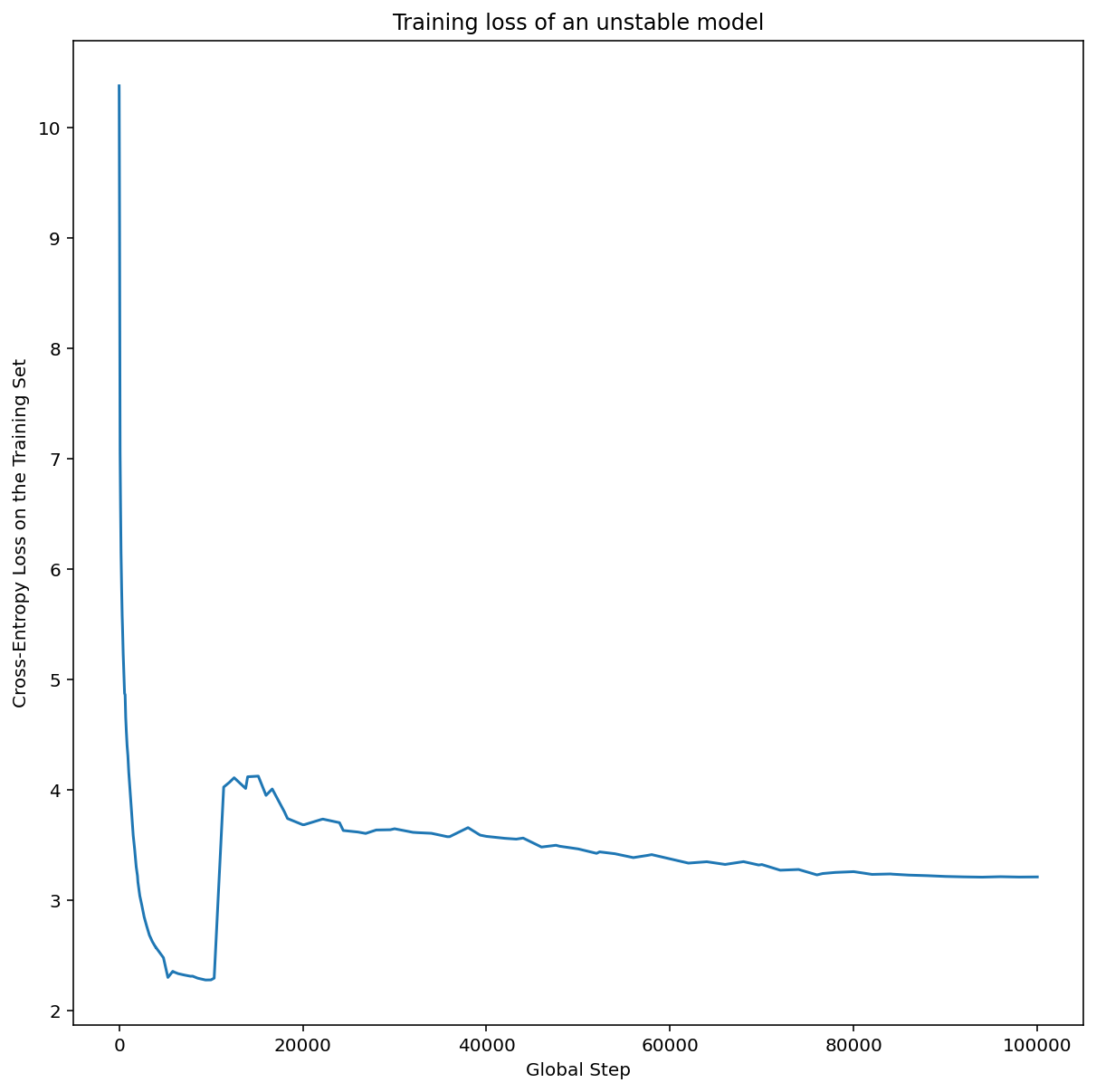
- Although we cannot enumerate them all, there are many other additional behaviors that can become evident from examining the training curves (e.g. training loss increasing during training usually indicates a bug in the training pipeline).
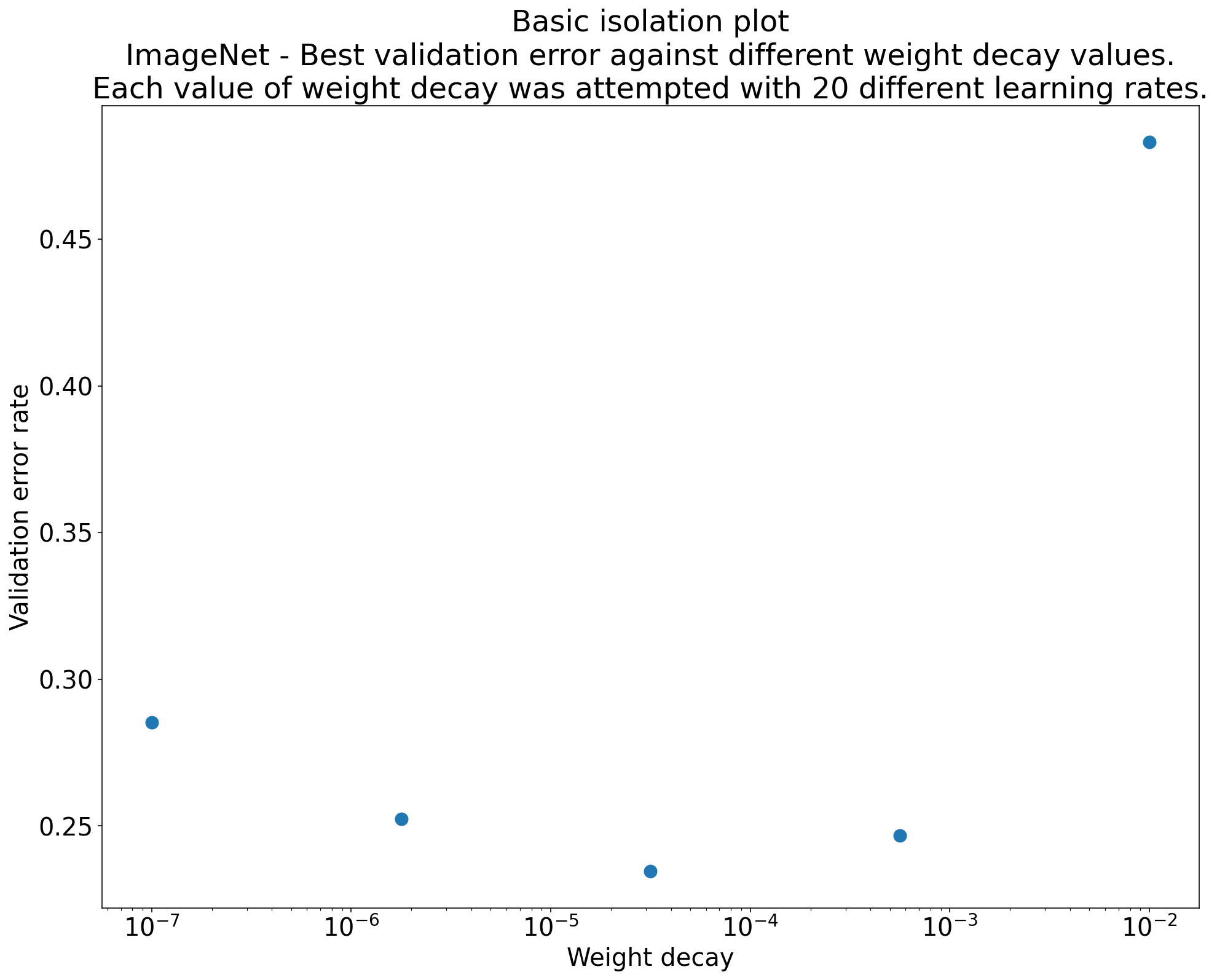
Detecting whether a change is useful with isolation plots
[Click to expand]
Figure 2: Isolation plot that investigates the best value of weight decay for ResNet-50 trained on ImageNet.
- Often, the goal of a set of experiments is to compare different values of a
scientific hyperparameter.
- For example, we may want to determine the value of weight decay that results in the best validation error.
- An isolation plot is a special case of the basic hyperparameter axis
plot. Each point on an isolation plot corresponds to the performance of the
best trial across some (or all) of the nuisance hyperparameters.
- In other words, we plot the model performance after "optimizing away" the nuisance hyperparameters.
- An isolation plot makes it easier to perform an apples-to-apples comparison between different values of the scientific hyperparameter.
- For example, Figure 2 reveals the value of weight decay that
produces the best validation performance for a particular configuration of
ResNet-50 trained on ImageNet.
- If our goal is to determine whether to include weight decay at all, then we would compare the best point from this plot against the baseline of no weight decay. For a fair comparison, the baseline should also have its learning rate equally well tuned.
- When we have data generated by (quasi)random search and are considering a continuous hyperparameter for an isolation plot, we can approximate the isolation plot by bucketing the x-axis values of the basic hyperparameter axis plot and taking the best trial in each vertical slice defined by the buckets.
Automate generically useful plots
[Click to expand]
- The more effort it is to generate plots, the less likely we are to look at them as much as we should, so it behooves us to set up our infrastructure to automatically produce as many of them as possible.
- At a minimum, we automatically generate basic hyperparameter axis plots for all hyperparameters that we vary in an experiment.
- Additionally, we automatically produce training curves for all trials and make it as easy as possible to find the best few trials of each study and examine their training curves.
- There are many other potential plots and visualizations we can add that can be useful. Although the ones described above are a good starting point, to paraphrase Geoffrey Hinton, "Every time you plot something new, you learn something new."
Determining whether to adopt a training pipeline change or hyperparameter configuration
Summary: When deciding whether to make a change to our model or training procedure or adopt a new hyperparameter configuration going forward, we need to be aware of the different sources of variation in our results.
- When we are trying to improve our model, we might observe that a particular
candidate change initially achieves a better validation error compared to
our incumbent configuration, but find that after repeating the experiment
there is no consistent advantage. Informally, we can group the most
important sources of variation that might cause such an inconsistent result
into the following broad categories:
-
Training procedure variance, retrain variance, or trial
variance: the variation we see between training runs that use the same
hyperparameters, but different random seeds.
- For example, different random initializations, training data shuffles, dropout masks, patterns of data augmentation operations, and orderings of parallel arithmetic operations, are all potential sources of trial variance.
-
Hyperparameter search variance, or study variance: the variation
in results caused by our procedure to select the hyperparameters.
- For example, we might run the same experiment with a particular search space, but with two different seeds for quasi-random search and end up selecting different hyperparameter values.
- Data collection and sampling variance: the variance from any sort of random split into training, validation, and test data or variance due to the training data generation process more generally.
-
Training procedure variance, retrain variance, or trial
variance: the variation we see between training runs that use the same
hyperparameters, but different random seeds.
- It is all well and good to make comparisons of validation error rates estimated on a finite validation set using fastidious statistical tests, but often the trial variance alone can produce statistically significant differences between two different trained models that use the same hyperparameter settings.
- We are most concerned about study variance when trying to make conclusions
that go beyond the level of an individual point in hyperparameters space.
- The study variance depends on the number of trials and the search space and we have seen cases where it is larger than the trial variance as well as cases where it is much smaller.
- Therefore, before adopting a candidate change, consider running the best
trial N times to characterize the run-to-run trial variance.
- Usually, we can get away with only recharacterizing the trial variance after major changes to the pipeline, but in some applications we might need fresher estimates.
- In other applications, characterizing the trial variance is too costly to be worth it.
- At the end of the day, although we only want to adopt changes (including new hyperparameter configurations) that produce real improvements, demanding complete certainty that something helps isn't the right answer either.
- Therefore, if a new hyperparameter point (or other change) gets a better
result than the baseline (taking into account the retrain variance of both
the new point and the baseline as best we can), then we probably should
adopt it as the new baseline for future comparisons.
- However, we should only adopt changes that produce improvements that outweigh any complexity they add.
After exploration concludes
Summary: Bayesian optimization tools are a compelling option once we’re done exploring for good search spaces and have decided what hyperparameters even should be tuned at all.
- At some point, our priorities will shift from learning more about the tuning problem to producing a single best configuration to launch or otherwise use.
- At this point, there should be a refined search space that comfortably contains the local region around the best observed trial and has been adequately sampled.
- Our exploration work should have revealed the most essential hyperparameters to tune (as well as sensible ranges for them) that we can use to construct a search space for a final automated tuning study using as large a tuning budget as possible.
- Since we no longer care about maximizing our insight into the tuning
problem, many of
the advantages of quasi-random search
no longer apply and Bayesian optimization tools should be used to
automatically find the best hyperparameter configuration.
- Open-Source Vizier implements a variety of sophisticated algorithms for tuning ML models, including Bayesian Optimization algorithms.
- If the search space contains a non-trivial volume of divergent points (points that get NaN training loss or even training loss many standard deviations worse than the mean), it is important to use black box optimization tools that properly handle trials that diverge (see Bayesian Optimization with Unknown Constraints for an excellent way to deal with this issue). Open-Source Vizier has support for divergent points by marking trials as infeasible, although it may not use our preferred approach from Gelbart et al., depending on how it is configured.
- At this point, we should also consider checking the performance on the test
set.
- In principle, we could even fold the validation set into the training set and retraining the best configuration found with Bayesian optimization. However, this is only appropriate if there won't be future launches with this specific workload (e.g. a one-time Kaggle competition).
Determining the number of steps for each training run
- There are two types of workloads: those that are compute-bound and those that are not.
- When training is compute-bound, training is limited by how long we are
willing to wait and not by how much training data we have or some other
factor.
- In this case, if we can somehow train longer or more efficiently, we should see a lower training loss and, with proper tuning, an improved validation loss.
- In other words, speeding up training is equivalent to improving training and the "optimal" training time is always "as long as we can afford."
- That said, just because a workload is compute-limited doesn't mean training longer/faster is the only way to improve results.
- When training is not compute-bound, we can afford to train as long as we
would like to, and, at some point, training longer doesn't help much (or
even causes problematic overfitting).
- In this case, we should expect to be able to train to very low training loss, to the point where training longer might slightly reduce the training loss, but will not meaningfully reduce the validation loss.
- Particularly when training is not compute-bound, a more generous
training time budget can make tuning easier, especially when tuning
learning rate decay schedules, since they have a particularly strong
interaction with the training budget.
- In other words, very stingy training time budgets might require a learning rate decay schedule tuned to perfection in order to achieve a good error rate.
- Regardless of whether a given workload is compute-bound or not, methods that
increase the variance of the gradients (across batches) will usually result
in slower training progress, and thus may increase the number of training
steps required to reach a particular validation loss. High gradient variance
can be caused by:
- Using a smaller batch size
- Adding data augmentation
- Adding some types of regularization (e.g. dropout)
Deciding how long to train when training is not compute-bound
- Our main goal is to ensure we are training long enough for the model to reach the best possible result, while avoiding being overly wasteful in the number of training steps.
- When in doubt, err on the side of training longer. Performance should never degrade when training longer, assuming retrospective (optimal) checkpoint selection is used properly and checkpoints are frequent enough.
- Never tune the
max_train_stepsnumber in a study. Pick a value and use it for all trials. From these trials, plot the training step that retrospective checkpoint selection finds in order to refine the choice ofmax_train_steps.- For example, if the best step is always during the first 10% of training, then the maximum number of steps is way too high.
- Alternatively, if the best step is consistently in the last 25% of training we might benefit from training longer and re-tuning the decay schedule.
- The ideal number of training steps can change when the architecture or data changes (e.g. adding data augmentation).
- Below we describe how to pick an initial candidate value for
max_train_stepsbased on the number of steps necessary to "perfectly fit" the training set using a constant learning rate.- Note, we are not using the phrase "perfectly fit the training set" in a
precise or mathematically well-defined way. It is merely meant as an
informal descriptor to indicate a very low training loss.
- For example, when training with the log loss, absent regularization terms, we might see the training loss keep slowly improving until we reach floating point limits as the network weights grow without bound and the predictions of the model on the training set become increasingly confident. In this case, we might say the model "perfectly fit" the training set around the time the misclassification error reached zero on the training set.
- The starting value for
max_train_stepswe find may need to be increased if the amount of gradient noise in the training procedure increases.- For example, if data augmentation or regularizers like dropout are introduced to the model.
- It may be possible to decrease
max_train_stepsif the training process improves somehow.- For example, with a better tuned optimizer or a better tuned learning rate schedule.
- Note, we are not using the phrase "perfectly fit the training set" in a
precise or mathematically well-defined way. It is merely meant as an
informal descriptor to indicate a very low training loss.
Algorithm for picking an initial candidate for max_train_steps using a learning rate sweep
[Click to expand]
- This procedure assumes it is possible to not only "perfectly" fit the training set, but to do so using a constant learning rate schedule.
- If it is possible to perfectly fit the entire training set, then there must
exist a configuration (with some value of
max_train_steps) that perfectly fits the training set; find any such configuration and use its value ofmax_train_stepsas a starting pointN. - Run a constant learning rate sweep (i.e. grid search the learning rate)
without data augmentation and without regularization where each trial trains
for
Nsteps. - The number of steps required for the fastest trial in the sweep to reach
perfect training performance is our initial guess for
max_train_steps. -
NOTE: Bad search spaces can make it possible to engage in
self-deception.
- For example, if all the learning rates in a study are too small, we
might incorrectly conclude that a very large value of
max_train_stepsis necessary. - At a minimum, we should check that the optimal learning rate in the study is not at the boundary of the search space.
- For example, if all the learning rates in a study are too small, we
might incorrectly conclude that a very large value of
Deciding how long to train when training is compute-bound
- In some cases, training loss keeps improving indefinitely and our patience and computational resources become the limiting factors.
- If training loss (or even validation loss) keeps improving indefinitely,
should we always train as long as we can afford? Not necessarily.
- We might be able to tune more effectively by running a larger number of shorter experiments and reserving the longest "production length" runs for the models we hope to launch.
- As the training time for trials approaches our patience limit, tuning experiments become more relevant for our potential launch candidates, but we can complete fewer of them.
- There are probably many questions we can answer while only training for ~10% of the production length, but there is always a risk that our conclusions at this time limit will not apply to experiments at 20% of the production length, let alone 100%.
- Tuning in multiple rounds with increasing, per-trial training step limits is
a sensible approach.
- We can do as many rounds as we want, but usually 1-3 are the most practical.
- Essentially, try to obtain as much understanding of the problem as possible using trials with a very quick turnaround time, trading off tuning thoroughness with relevance to the final, longest runs.
- Once a given per-trial time limit has generated useful insights, we can increase the training time and continue tuning, double-checking our conclusions from the shorter runs as needed.
- As a starting point, we recommend two rounds of tuning:
- Round 1: Shorter runs to find good model and optimizer hyperparameters.
- Round 2: Very few long runs on good hyperparameter points to get the final model.
- The biggest question going from
Round i→Round i+1is how to adjust learning rate decay schedules.- One common pitfall when adjusting learning rate schedules between rounds is using all the extra training steps with too small of a learning rate.
Round 1
[Click to expand]
- Unfortunately, there is no guarantee that good hyperparameters found in short, incomplete training are still good choices when training length is significantly increased. However, for some kinds of hyperparameters, they are often correlated enough for Round 1 to be useful.
- What hyperparameter values found in shorter runs do we expect to transfer to
longer training runs? For all of this, we need more research. But based on
what we know so far, here are the authors’ suspicions in order of decreasing
probability of transferring:
- Very likely to transfer
- Early training instability can be resolved in the first round of
tuning using a smaller number of training steps. Perhaps these
hyperparameters are the closest thing to a sure bet for transfer
that we have.
- Warmup length
- Initialization
- Early training instability can be resolved in the first round of
tuning using a smaller number of training steps. Perhaps these
hyperparameters are the closest thing to a sure bet for transfer
that we have.
- Likely to transfer
- Model architecture - A dramatic win in the model architecture will usually transfer, but there are probably many counterexamples.
- Might transfer
- Optimization algorithm/optimizer hyperparameters - We think this would "loosely" transfer. It’s definitely weaker than the things above it.
- Data augmentation
- Regularization
- If it isn't possible to perfectly fit the training set, the model might be in a regime where regularization is unlikely to help very much.
- Unlikely to transfer
- Learning rate schedule: unlikely to transfer perfectly.
-
This paper suggests that
even decay schedule transfers, but we don't believe this is true
in general. Example: Tuning sqrt decay on small # of training
steps then extending to large # will result in the majority of
training occurring at overly small steps.
- One can likely do "good enough" with most schedules in the limit of extreme training budget, but noticeable performance improvements can likely be seen if it is tuned.
- Understanding Short-Horizon Bias in Stochastic Meta-Optimization describes the dangers of trying to pick learning rates myopically.
-
This paper suggests that
even decay schedule transfers, but we don't believe this is true
in general. Example: Tuning sqrt decay on small # of training
steps then extending to large # will result in the majority of
training occurring at overly small steps.
- Learning rate schedule: unlikely to transfer perfectly.
- Very likely to transfer
Round 2
[Click to expand]
- Run the best hyperparameter configuration from Round 1.
-
(Speculation) 🤖 Use the extra steps to extend the period of training at
a high learning rate.
- E.g. if linear schedule then keep the length of the decay fixed from Round 1 and extend the period of constant lr in the beginning.
- For cosine decay, just keep the base lr from Round 1 and extend
max_train_stepsas in Chinchilla paper.
- More rounds might make sense for teams with very mature modeling and tuning
pipelines and very long and expensive production training runs, but they
will often be overkill.
- We've described how to transfer from Step 1 → Step 2. If we didn't care
about analysis time and if making efficient use of compute was the
overriding concern, then the ideal would be to exponentially increase
the length of training runs (and thus the end-to-end time to complete a
study) over many different rounds of tuning.
- At each round we systematically ensure our choices continue to hold up.
- New ideas go through a pipeline that progressively derisks them using increasingly long-running experiments from Step i to Step i+1.
- We've described how to transfer from Step 1 → Step 2. If we didn't care
about analysis time and if making efficient use of compute was the
overriding concern, then the ideal would be to exponentially increase
the length of training runs (and thus the end-to-end time to complete a
study) over many different rounds of tuning.
Additional guidance for the training pipeline
Optimizing the input pipeline
Summary: The causes and interventions of input-bound pipelines are highly task-dependent; use a profiler and look out for common issues.
- Use an appropriate profiler to diagnose input-bound pipelines. For example, Perfetto for JAX or TensorFlow profiler for TensorFlow.
- Ultimately, the specific causes and interventions will be highly task-dependent. Broader engineering considerations (e.g. minimizing disk footprint) may warrant worse input pipeline performance.
- Common causes:
- Data are not colocated with the training process, causing I/O latency (this might happen when reading training data over a network).
- Expensive online data preprocessing (consider doing this once offline and saving).
- Unintentional synchronization barriers that interfere with data pipeline prefetching. For example, when synchronizing metrics between the device and host in CommonLoopUtils (link).
- Common tips:
- Instrument input pipeline to prefetch examples (e.g. tf.data.Dataset.prefetch)
- Remove unused features/metadata from each as early in the pipeline as possible.
- Increase the replication of the number of jobs generating examples for the input pipeline. For example, by using the tf.data service.
Evaluating model performance
Summary: Run evaluation at larger batch sizes than training. Run evaluations at regular step intervals, not regular time intervals.
Evaluation settings
[Click to expand]
- There are several settings in which we can evaluate the performance of our
models.
- Online evaluation - metrics are collected when the model is serving predictions in a production environment.
- Offline evaluation - metrics are collected when the model is run on offline train/validation/test sets that are representative of the production environment.
- Periodic evaluations - metrics are collected during model training that might either be a proxy for the offline evaluation, and/or on a subset of the data used in offline evaluation.
- Online evaluation is the gold standard, but is often impractical during the model development phase.
- Depending on the problem, offline evaluation can be fairly involved and computationally expensive.
- Periodic evaluations are the most practical and economical choice, but may
not fully represent the production environment.
- Our goal during periodic evaluation is to use an expedient proxy of the offline evaluation, without sacrificing the reliability of the signal we get during training.
Setting up periodic evaluations
[Click to expand]
- We run periodic evaluations during training to monitor its progress in real time, to facilitate retrospective model checkpoint selection, and so that we can examine the training curves at the end of training.
- The simplest configuration is to perform both training and periodic
evaluations within the same compute instance, periodically alternating
between training and evaluation.
- In this case, the batch size used to perform evaluations should be at least as large as the batch size used for training because model activations don't need to be maintained during evaluation, lowering the computational requirements per example.
- Periodic evaluations should be done at regular step intervals, not time
intervals.
- Evaluating based on time intervals can make it harder to interpret the training curves, especially when training may suffer from preemptions of the training jobs, network latency issues, etc.
- Periodicity in valid/test metrics (when using a shuffled train/validation/test split) can indicate implementation bugs such as test data having overlap with training data, or training data not being properly shuffled. Evaluating at regular step intervals can make these issues easier to catch.
- Partial batches can occur when the evaluation sets are not divisible by the batch size. Ensure that the padded examples are correctly weighted to prevent the loss function from being biased by them. Often, these padded examples can be given a weight of zero.
- Save sufficient information per evaluation to support offline analysis.
Ideally, we would save predictions on a selection of individual examples
since they can be invaluable for debugging.
- Generating artifacts like SavedModels make it easy to do ad-hoc model inspection after evaluation jobs finish.
Choosing a sample for periodic evaluation
[Click to expand]
- The periodic evaluation job might not run fast enough to compute metrics on the full offline evaluation set in a reasonable amount of time. This often necessitates sampling data for periodic evaluation.
- We consider the following factors when constructing a sampled dataset:
-
Sample size
- Check that the performance computed on the sampled dataset used by the periodic job matches the performance on the whole offline evaluation set, i.e. there is no skew between the sampled set and the full dataset.
- The dataset used for periodic evaluation should be small enough that it’s easy to generate model predictions over its entirety, but large enough that improvements to the model can be accurately measured (i.e. not overwhelmed by label noise).
- It should be large enough to accommodate multiple such evaluations across trials in sequence, and still produce accurate estimates. That is, to avoid adaptively "fitting" to the validation set over time, in a way that doesn't generalize to a held-out test set. However, this consideration is rarely a practical concern.
-
Imbalanced datasets
- For imbalanced datasets, performance on rare classes of examples will often be noisy.
- For datasets with a small number of examples in a class label, log the number of examples predicted correctly to get more insight into accuracy improvements (.05 sensitivity improvement sounds exciting, but was it just one more example correct?).
-
Sample size
Saving checkpoints and retrospectively selecting the best checkpoint
Summary: Run training for a fixed number of steps and retrospectively choose the best checkpoint from the run.
- Most deep learning frameworks support model checkpointing. That is, the current state of the model is periodically preserved on disk. This allows the training job to be resilient to compute instance interruptions.
- The best checkpoint is often not the last checkpoint, particularly when the validation set performance does not continue to increase over time but rather fluctuates about a particular value.
- Set up the pipeline to keep track of the N best checkpoints seen so far during training. At the end of training, model selection is then a matter of choosing the best checkpoint seen during training. We call this retrospective optimal checkpoint selection.
- Supporting prospective early stopping is usually not necessary, since we’re pre-specifying a trial budget and are preserving the N best checkpoints seen so far.
Setting up experiment tracking
Summary: When tracking different experiments, make sure to note a number of essentials like the best performance of a checkpoint in the study, and a short description of the study.
- We've found that keeping track of experiment results in a spreadsheet has
been helpful for the sorts of modeling problems we've worked on. It often
has the following columns:
- Study name
- A link to wherever the config for the study is stored.
- Notes or a short description of the study.
- Number of trials run
- Performance on the validation set of the best checkpoint in the study.
- Specific reproduction commands or notes on what unsubmitted changes were necessary to launch training.
- Find a tracking system that captures at least the information listed above and is convenient for the people doing it. Untracked experiments might as well not exist.
Batch normalization implementation details
Summary: Nowadays batch norm can often be replaced with LayerNorm, but in cases where it cannot, there are tricky details when changing the batch size or number of hosts.
- Batch norm normalizes activations using their mean and variance over the current batch, but in the multi-device setting these statistics are different on each device unless explicitly synchronized.
- Anecdotal reports (mostly on ImageNet) say calculating these normalizing statistics using only ~64 examples actually works better in practice (see Ghost Batch Norm from this paper).
- Decoupling the total batch size and the number of examples used to calculate batch norm statistics is particularly useful for batch size comparisons.
- Ghost batch norm implementations do not always correctly handle the case where the per-device batch size > virtual batch size. In this case we'd actually need to subsample the batch on each device in order to get the proper number of batch norm statistic examples.
- Exponential moving averages used in test mode batch norm are just a linear combination of training statistics, so these EMAs only need to be synchronized before saving them in checkpoints. However, some common implementations of batch norm do not synchronize these EMAs and only save the EMA from the first device.
Considerations for multi-host pipelines
Summary: for logging, evals, RNGs, checkpointing, and data sharding, multi-host training can make it very easy to introduce bugs!
- Ensure the pipeline is only logging and checkpointing on one host.
- Make sure before evaluation or checkpointing is run, the batch norm statistics are synchronized across hosts.
- It is critical to have RNG seeds that are the same across hosts (for model initialization), and seeds that are different across hosts (for data shuffling/preprocessing), so make sure to mark them appropriately.
- Sharding data files across hosts is usually recommended for improved performance.
FAQs
What is the best learning rate decay schedule family?
[Click to expand]
- It’s an open problem. It’s not clear how to construct a set of rigorous experiments to confidently answer what the "best" LR decay schedule is.
- Although we don't know the best schedule family, we're confident that it’s important to have some (non-constant) schedule and that tuning it matters.
- Different learning rates work best at different times during the optimization process. Having some sort of schedule makes it more likely for the model to hit a good learning rate.
Which learning rate decay should I use as a default?
[Click to expand]
- Our preference is either linear decay or cosine decay, and a bunch of other schedule families are probably good too.
Why do some papers have complicated learning rate schedules?
[Click to expand]
- It’s not uncommon to see papers with complicated piecewise learning rate (LR) decay schedules.
- Readers often wonder how the authors arrived at such a complicated schedule.
- Many complicated LR decay schedules are the result of tuning the schedule as
a function of the validation set performance in an ad hoc way:
- Start a single training run with some simple LR decay (or a constant learning rate).
- Keep training running until the performance seems to stagnate. If this happens, pause training. Resume it with a perhaps steeper LR decay schedule (or smaller constant learning rate) from this point. Repeat this process until the conference/launch deadline.
- Blithely copying the resulting schedule is generally not a good idea since
the best particular schedule will be sensitive to a host of other
hyperparameter choices.
- Better to copy the algorithm that produced the schedule, although this is rarely possible when arbitrary human judgment produced the schedule.
- This type of validation-error-sensitive schedule is fine to use if it can be
fully automated, but human-in-the-loop schedules that are a function of
validation error are brittle and not easily reproducible, so we recommend
avoiding them.
- Before publishing results that used such a schedule, please try to make it fully reproducible.
How should Adam’s hyperparameters be tuned?
[Click to expand]
- As discussed above, making general statements about search spaces and how
many points one should sample from the search space is very difficult. Note
that not all the hyperparameters in Adam are equally important. The
following rules of thumb correspond to different "budgets" for the number of
trials in a study.
- If < 10 trials in a study, only tune the (base) learning rate.
- If 10-25 trials, tune learning rate and $\beta_1$.
- If 25+ trials, tune the learning rate, $\beta_1$ and $\epsilon$.
- If one can run substantially more than 25 trials, additionally tune $\beta_2$.
Why use quasi-random search instead of more sophisticated black box optimization algorithms during the exploration phase of tuning?
[Click to expand]
- Quasi-random search (based on low-discrepancy sequences) is our preference over fancier black box optimization tools when used as part of an iterative tuning process intended to maximize insight into the tuning problem (what we refer to as the "exploration phase"). Bayesian optimization and similar tools are more appropriate for the exploitation phase.
- Quasi-random search based on randomly shifted low-discrepancy sequences can be thought of as "jittered, shuffled grid search", since it uniformly, but randomly, explores a given search space and spreads out the search points more than random search.
- The advantages of quasi-random search over more sophisticated black box
optimization tools (e.g. Bayesian optimization, evolutionary algorithms)
include:
- Sampling the search space non-adaptively makes it possible to change the
tuning objective in post hoc analysis without rerunning experiments.
- For example, we usually want to find the best trial in terms of validation error achieved at any point in training. But the non-adaptive nature of quasi-random search makes it possible to find the best trial based on final validation error, training error, or some alternative evaluation metric without rerunning any experiments.
- Quasi-random search behaves in a consistent and statistically
reproducible way.
- It should be possible to reproduce a study from six months ago even if the implementation of the search algorithm changes, as long as it maintains the same uniformity properties. If using sophisticated Bayesian optimization software, the implementation might change in an important way between versions, making it much harder to reproduce an old search. It isn’t always possible to roll back to an old implementation (e.g. if the optimization tool is run as a service).
- Its uniform exploration of the search space makes it easier to reason
about the results and what they might suggest about the search space.
- For example, if the best point in the traversal of quasi-random search is at the boundary of the search space, this is a good (but not foolproof) signal that the search space bounds should be changed. This section goes into more depth. However, an adaptive black box optimization algorithm might have neglected the middle of the search space because of some unlucky early trials even if it happens to contain equally good points, since it is this exact sort of non-uniformity that a good optimization algorithm needs to employ to speed up the search.
- Running different numbers of trials in parallel versus sequentially will not produce statistically different results when using quasi-random search (or other non-adaptive search algorithms), unlike with adaptive algorithms.
- More sophisticated search algorithms may not always handle infeasible points correctly, especially if they aren't designed with neural network hyperparameter tuning in mind.
- Quasi-random search is simple and works especially well when many tuning
trials will be running in parallel.
- Anecdotally1, it is very hard for an adaptive algorithm to beat a quasi-random search that has 2X its budget, especially when many trials need to be run in parallel (and thus there are very few chances to make use of previous trial results when launching new trials).
- Without expertise in Bayesian optimization and other advanced black box optimization methods, we might not achieve the benefits they are, in principle, capable of providing. It is hard to benchmark advanced black box optimization algorithms in realistic deep learning tuning conditions. They are a very active area of current research, and the more sophisticated algorithms come with their own pitfalls for inexperienced users. Experts in these methods are able to get good results, but in high-parallelism conditions the search space and budget tend to matter a lot more.
- Sampling the search space non-adaptively makes it possible to change the
tuning objective in post hoc analysis without rerunning experiments.
- That said, if our computational resources only allow a small number of trials to run in parallel and we can afford to run many trials in sequence, Bayesian optimization becomes much more attractive despite making our tuning results harder to interpret.
Where can I find an implementation of quasi-random search?
[Click to expand]
-
Open-Source Vizier has an implementation
of quasi-ranom search. Set
algorithm="QUASI_RANDOM_SEARCH"in this usage example. - An alternative implementation exists here.
- Both implementations above generate a Halton sequence for a given search space (intended to implement a shifted, scrambled Halton sequence as recommended in https://arxiv.org/abs/1706.03200).
- If a quasi-random search algorithm based on a low-discrepancy sequence is
not available, it is possible to substitute pseudo random uniform search
instead, although this is likely to be slightly less efficient.
- In 1-2 dimensions, grid search is also acceptable, although not in higher dimensions (see Bergstra & Bengio, 2012).
How many trials are needed to get good results with quasi-random search?
[Click to expand]
Figure 3: A ResNet-50 was tuned on ImageNet with 100 trials. Via bootstrapping, different amounts of tuning budget were simulated. Box plots of the best performances for each trial budget are plotted above.
- There is no way to answer this question in general, but we can look at specific examples.
- As the Figure 3 shows, the number of trials in a study can have a
substantial impact on the results.
- Notice how large the interquartile ranges are when 6 trials were sampled, versus when 20 trials were sampled.
- Even with 20 trials, it is likely that the difference between especially lucky and unlucky studies will be larger than the typical variation between re-trains of this model on different random seeds, with fixed hyperparameters, which for this workload might be around +/- 0.1% on a validation error rate of ~23%.
How can optimization failures be debugged and mitigated?
[Click to expand]
Summary: If the model is experiencing optimization difficulties, it’s important to fix them before trying other things. Diagnosing and correcting training failures is an active area of research.
Figure 4: Changing the strides in a single residual block (2x2 -> 1x1) in a WideResnet results in training instability. This does not degrade performance at low learning rates, but high learning rates no longer train well due to the instability. Applying 1000 steps of learning rate warmup resolves this particular instance of instability, allowing stable training at max learning rate of .1.
Identifying unstable workloads
- Any workload will become unstable if the learning rate is too large. Instability is only an issue when it forces us to use a learning rate that’s too small.
- There are at least two types of training instability worth distinguishing:
- Instability at initialization/early in training.
- Sudden instability in the middle of training.
- We can take a systematic approach to identifying stability issues in our
workload.
- Do a learning rate sweep and find the best learning rate lr*.
- Plot training loss curves for learning rates just above lr*.
- If the learning rates > lr* show loss instability (loss goes up not down during periods of training), then it is likely that fixing the instability will result in better training.
- Log the L2 norm of the full loss gradient during training, outlier values can result in spurious instability in the middle of training. This can inform how to pick gradient/update clipping.
NOTE: Some models show very early instability followed by a recovery that results in slow but stable training. Common evaluation schedules can miss these issues by not evaluating frequently enough!
To check for this, we can train for an abbreviated run of just ~500 steps using
lr = 2 * current best, but evaluate every step.
Figure 5: Illustration of the value of more frequent evaluations at the start of training. Useful if there’s a suspicion that the model suffers from early training instability.
Potential fixes for common instability patterns
- Apply learning rate warmup
- Best for early training instability.
- Apply gradient clipping
- Good for both early and mid training instability, may fix some bad inits that warmup cannot.
- Try a new optimizer
- Sometimes Adam can handle instabilities that Momentum can’t. This is an active area of research.
- We can ensure that we’re using best practices/initializations for our model
architecture (examples below).
- Add residual connections and normalization if the model doesn't contain it already.
- Normalization should be the last operation before the residual. E.g. x + Norm(f(x)).
- Norm(x + f(x)) known to cause issues.
- Try initializing residual branches to 0 (e.g. ReZero init).
- Lower the learning rate
- This is a last resort.
Learning rate warmup
Figure 6: An example of instability during a warmup period (note the horizontal axis log scale). 40k steps of warmup was needed for successful training in this case.
When to apply learning rate warmup
Figure 7a: An example of a hyperparameter axis plot for a model exhibiting training instability. The best learning rate is at the edge of what is feasible. An "infeasible" trial is defined as one that either produces NaNs or uncharacteristically high values of the loss.
Figure 7b: The training loss of a model trained with a learning rate where we see instability.
- Figure 7a shows a hyperparameter axis plot that indicates a model experiencing optimization instabilities, because the best learning rate is right at the edge of instability.
- Figure 7b shows how this can be double-checked by examining the training loss of a model trained with a learning rate either 5x or 10x larger than this peak. If that plot shows a sudden rise in the loss after a steady decline (e.g. at step ~10k in the figure above), then the model likely suffers from optimization instability.
How to apply learning rate warmup
Figure 8: Beneficial effect of learning rate warmup on addressing training instabilities.
- Using the section immediately above, we assume that the practitioner has
already identified the learning rate at which the model becomes unstable.
This is the
unstable_base_learning_rate. - Warmup involves prepending a learning rate schedule that ramps up the
learning rate from 0 to some stable
base_learning_rate, that is at least one order of magnitude larger thanunstable_base_learning_rate. The default would be to try abase_learning_ratethat’s 10xunstable_base_learning_rate. Although note that it’d be possible to run this entire procedure again for something like 100xunstable_base_learning_rate. The specific schedule is:- Ramp up from 0 to
base_learning_rateoverwarmup_steps. - Train at a constant rate for
post_warmup_steps.
- Ramp up from 0 to
- Our goal is to find the shortest number of
warmup_stepsthat allows us to access peak learning rates that are much higher thanunstable_base_learning_rate. - So for each
base_learning_rate, we need to tunewarmup_stepsandpost_warmup_steps. It’s usually fine to setpost_warmup_stepsto be2*warmup_steps. - Warmup can be tuned independently of an existing decay schedule.
warmup_stepsshould be swept at a few different orders of magnitude. For example, an example study could try [10, 103, 104, 105]. The largest feasible point shouldn't be more than 10% ofmax_train_steps. - Once a
warmup_stepsthat doesn't blow up training atbase_learning_ratehas been established, it should be applied to the baseline model. Essentially, we prepend this schedule onto the existing schedule, and use the optimal checkpoint selection discussed above to compare this experiment to the baseline. For example, if we originally had 10,000max_train_stepsand didwarmup_stepsfor 1000 steps, the new training procedure should run for 11,000 steps total. - If long
warmup_stepsare required for stable training (>5% ofmax_train_steps),max_train_stepsmay need to be increased to account for this. - There isn't really a "typical" value across the full range of workloads. Some models only need 100 steps, while others (particularly transformers) may need 40k+.
Gradient clipping
Figure 9: Illustration of gradient clipping correcting early training instability.
- Gradient clipping is most useful when large or outlier gradient issues occur.
- Clipping can fix either early training instability (large gradient norm early), or mid training instabilities (sudden gradient spikes mid training).
- Sometimes longer warmup periods can correct instabilities that clipping does
not: see this section above.
- 🤖 What about clipping during warmup?
- The ideal clip thresholds are just above the "typical" gradient norm.
- Here’s an example of how gradient clipping could be done:
- If the norm of the gradient $\left | g \right |$ is greater than the gradient clipping threshold $\lambda$, then do ${g}'= \lambda \times \frac{g}{\left | g \right |}$ where ${g}'$ is the new gradient.
- Log the unclipped gradient norm during training. By default, generate:
- A plot of gradient norm vs step
- A histogram of gradient norms aggregated over all steps
- Choose a gradient clipping threshold based on the 90th percentile of
gradient norms.
- The threshold will be workload dependent, but 90% is a good starting point. If it doesn't work, this threshold can be tuned.
- 🤖 What about some sort of adaptive strategy?
- If we try gradient clipping and the instability issues remain, we can try it harder (i.e. make the threshold smaller).
- Extremely aggressive gradient clipping is in essence a strange way of reducing the learning rate. If we find ourselves using extremely aggressive clipping, we probably should just cut the learning rate instead.
- We would usually consider having >50% of the updates getting clipped somehow as "extremely aggressive".
- If we need to do extremely aggressive gradient clipping to deal with our instability issues, then we might as well reduce the learning rate.
Why do you call the learning rate and other optimization parameters hyperparameters? They are not parameters of any prior distribution.
[Click to expand]
- It is true that the term "hyperparameter" has a precise meaning in Bayesian machine learning and referring to the learning rate and most of the other parameters we tune in deep learning as "hyperparameters" is an abuse of terminology.
- We would prefer to use the term "metaparameter" for learning rates, architectural parameters, and all the other things we tune in deep learning, since it avoids the potential for confusion that comes from misusing the word "hyperparameter" (confusion that is especially likely when discussing Bayesian optimization where the probabilistic response surface models have their own true hyperparameters).
- Unfortunately, although potentially confusing, the term hyperparameter has become extremely common in the deep learning community.
- Therefore, for a document, such as this one, intended for a wide audience that includes many people who are unlikely to be aware of this technicality, we made the choice to contribute to one source of confusion in the field in hopes of avoiding another.
- That said, we might make a different choice when publishing a research paper, and we would encourage others to use "metaparameter" instead in most contexts.
Why shouldn't the batch size be tuned to directly improve validation set performance?
[Click to expand]
- Changing the batch size without changing any other details of the training pipeline will often affect the validation set performance.
- However, the difference in validation set performance between two batch sizes typically goes away if the training pipeline is optimized independently for each batch size.
- The hyperparameters that interact most strongly with the batch size, and therefore are most important to tune separately for each batch size, are the optimizer hyperparameters (e.g. learning rate, momentum) and the regularization hyperparameters.
- Smaller batch sizes introduce more noise into the training algorithm due to sample variance, and this noise can have a regularizing effect. Thus, larger batch sizes can be more prone to overfitting and may require stronger regularization and/or additional regularization techniques.
- In addition, the number of training steps may need to be adjusted when changing the batch size.
- Once all these effects are taken into account, there is currently no convincing evidence that the batch size affects the maximum achievable validation performance (see Shallue et al. 2018).
What are the update rules for all the popular optimization algorithms?
[Click to expand]
Stochastic gradient descent (SGD)
$$\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)$$
Momentum
$$v_0 = 0$$
$$v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)$$
$$\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}$$
Nesterov
$$v_0 = 0$$
$$v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)$$
$$\theta_{t+1} = \theta_{t} - \eta_t( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t})$$
RMSProp
$$v_0 = 1 \text{,} m_0 = 0$$
$$v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2$$
$$m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)$$
$$\theta_{t+1} = \theta_{t} - m_{t+1}$$
ADAM
$$m_0 = 0 \text{,} v_0 = 0$$
$$m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)$$
$$v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2$$
$$b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}$$
$$\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}$$
NADAM
$$m_0 = 0 \text{,} v_0 = 0$$
$$m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)$$
$$v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2$$
$$b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}$$
$$\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}$$
Acknowledgments
- We owe a debt of gratitude to Max Bileschi, Roy Frostig, Zelda Mariet, Stan Bileschi, Mohammad Norouzi, Chris DuBois and Charles Sutton for reading the manuscript and providing valuable feedback.
- We reused some experimental data for several plots that were originally produced by Naman Agarwal for other joint research.
- We would like to thank Will Chen for invaluable advice on the presentation of the document.
- We would also like to thank Rohan Anil for useful discussions.
Citing
@misc{tuningplaybookgithub,
author = {Varun Godbole and George E. Dahl and Justin Gilmer and Christopher J. Shallue and Zachary Nado},
title = {Deep Learning Tuning Playbook},
url = {http://github.com/google-research/tuning_playbook},
year = {2023},
note = {Version 1.0}
}
Contributing
-
This is not an officially supported Google product.
-
We'd love to hear your feedback!
- If you like the playbook, please leave a star! Or email deep-learning-tuning-playbook [at] googlegroups.com. Testimonials help us justify creating more resources like this.
- If anything seems incorrect, please file an issue to start a discussion. For questions or other messages where an issue isn't appropriate, please open a new discussion topic on GitHub.
-
As discussed in the preamble, this is a living document. We anticipate making periodic improvements, both small and large. If you’d like to be notified, please watch our repository (see instructions).
-
Please don't file a pull request without first coordinating with the authors via the issue tracking system.
Contributor License Agreement
Contributions to this project must be accompanied by a Contributor License Agreement (CLA). You (or your employer) retain the copyright to your contribution; this simply gives us permission to use and redistribute your contributions as part of the project. Head over to https://cla.developers.google.com/ to see your current agreements on file or to sign a new one.
You generally only need to submit a CLA once, so if you've already submitted one (even if it was for a different project), you probably don't need to do it again.
Code Reviews
All submissions, including submissions by project members, require review. We use GitHub pull requests for this purpose. Consult GitHub Help for more information on using pull requests.
Community Guidelines
This project follows Google's Open Source Community Guidelines.
-
Ben Recht and Kevin Jamieson pointed out how strong 2X-budget random search is as a baseline (the Hyperband paper makes similar arguments), but it is certainly possible to find search spaces and problems where state-of-the-art Bayesian optimization techniques crush random search that has 2X the budget. However, in our experience beating 2X-budget random search gets much harder in the high-parallelism regime since Bayesian optimization has no opportunity to observe the results of previous trials. ↩